For this meeting the main material is introduction of tree in data structures and this material is lectured by miss rulyna .
TREE
A tree data structure can be defined recursively (locally) as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the “children”), with the constraints that no reference is duplicated, and none points to the root.
EXP:
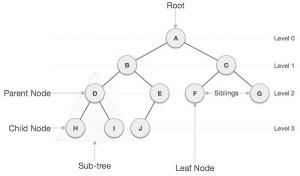
Terminologies used in Trees
Path − Path refers to sequence of nodes along the edges of a tree.
Root − Node at the top of the tree is called root. There is only one root per tree and one path from root node to any node.
Parent − Any node except root node has one edge upward to a node called parent.
Child − Node below a given node connected by its edge downward is called its child node.
Leaf − Node which does not have any child node is called leaf node.
Subtree − Subtree represents descendents of a node.
Visiting − Visiting refers to checking value of a node when control is on the node.
Traversing − Traversing means passing through nodes in a specific order.
Levels − Level of a node represents the generation of a node. If root node is at level 0, then its next child node is at level 1, its grandchild is at level 2 and so on.
keys − Key represents a value of a node based on which a search operation is to be carried out for a node.
HOW TO DETERMINE
2^k = Is to determine the nodes can be fit in a tree.
n-1= Is to determine the max number of level in a tree(n=nodes).
2log(n)= Is to determine the max number of level in a tree(n=nodes).
2^kh-1= Is to determine max number of nodes in a tree.
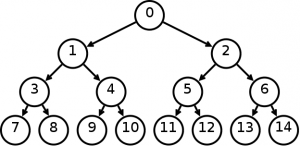
BINARY TREE
A binary tree is made of nodes, where each node contains a “left” pointer, a “right” pointer, and a data element. The “root” pointer points to the topmost node in the tree. The left and right pointers recursively point to smaller “subtrees” on either side. A null pointer represents a binary tree with no elements — the empty tree. The formal recursive definition is: a binary tree is either empty (represented by a null pointer), or is made of a single node, where the left and right pointers (recursive definition ahead) each point to a binary tree.
binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child. A recursive definition using just set theory notions is that a (non-empty) binary tree is a triple (L, S, R), where L and R are binary trees or the empty set and S is a singleton set.
EXP