today lesson is gonna more talk about Red Black Tree(RBT) and 2-3 tree that will be explained by the lecturer miss rulyna.
red–black tree(RBT) is a kind of self-balancing binary search tree. Each node of the binary tree has an extra bit, and that bit is often interpreted as the color (red or black) of the node. These color bits are used to ensure the tree remains approximately balanced during insertions and deletions.
RBT rules
1.Insertion
If you want to insert a node in a RBT is very similar insertion like BST only a minor changes like :
- A root of a node have to be black.
- the leaf of a RBT have to had red color
*if you don’t follow these rules your tree must have a violation that have to be fixed in order to balance the tree.
2.Delete
to delete the nodes is use the same principal like BST but the difference is you have to follow those violation rules to balance out your RBT.
Clik here to see RBT visualization
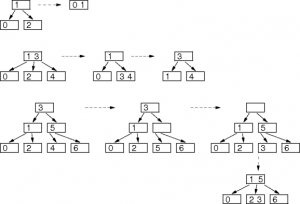
2-3 Tree is a tree data structure, where every node with children (internal node) has either two children (2-node) and one data element or three children (3 nodes) and two data elements. According to Knuth, “a B-tree of order 3 is a 2-3 tree.” Nodes on the outside of the tree (leaf nodes) have no children and one or two data elements. 2−3 trees were invented by John Hopcroft in 1970. 2-3 tree is not categorized as a BST tree.
Rules:
1. 2-3 has 3 key in 1 node.
2. Max child of the tree is 3.
3.The calculation is (n-1/2).
4.every leaf have the same level
Insertion
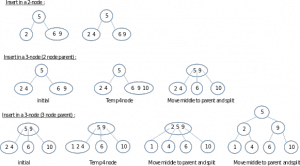
to insert the nodes first you must determine witch key should be put correctly :
1.smallest amount key on the left.
2.the larger amount key put to the right.
3.the middle key is the amount between the smallest and the large ones
after the key is full you can add another node .
Note: to balance the 2-3 tree you need to pull some of the amount of key in the root to balance out the tree or you can push the amount of key to the root to fill the root node and balance it out .
Delete
To delete a tree first you must find the replacement for the deletion of the tree
1.If the leaf node is 2 – node , if the sibling is a 3 – node , then take one key from one parent and one sibling in a push data from node to a parent .
2.If the leaf node is a 3 – node the the key from the first parent.
3.If the sibling of the leaf node is a 3 – node , then do push 1 data from the sibling to parent.
4.If the sibling of the leaf node is 2 – node , then the parent should be changed to a 2- node , and then do a merge between leaf nodes and sibling nodes.
do it until the 2-3 tree is balance