Month: May 2016

today lesson is gonna talk about heap ,tries ,hashing that will be explained by the lecturer pak sky.

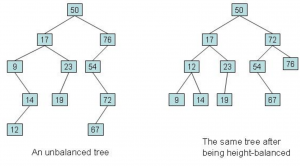
Heap
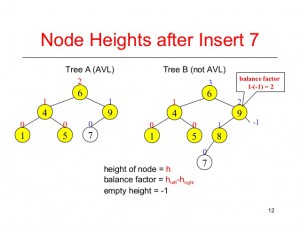
In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: If A is a parent node of B then the key (the value) of node A is ordered with respect to the key of node B with the same ordering applying across the heap.

There are 3 kind of heap

1.Max-heap
is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node.The value of the root have to be greater than any other nodes.

2.Min-Heap
is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node.The value of the root have to be smallest than any other nodes.

Min-Max Heap
is a double-ended priority queue implemented as a modified version of a binary heap. Like a binary heap, a min-max heap is represented as a complete binary tree.

Heap Majorly has 3 operations
-Insert Oper­a­tion
-Delete Oper­a­tion
-Extract-Min (OR Extract-Max)/not discussed on today lecture.

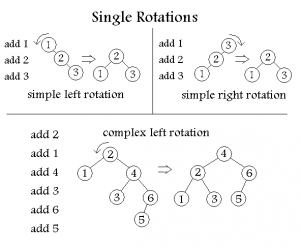
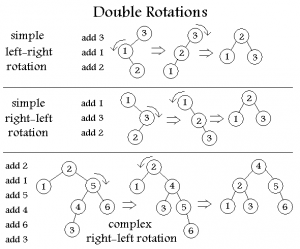
Insertion:
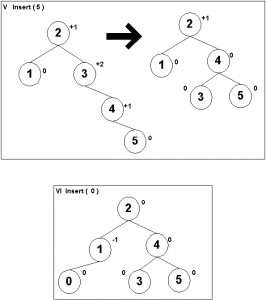
1. Add the element at the bottom leaf of the Heap.
2. Perform the Bubble-Up operation.
3.All Insert operations must perform the bubble-up operations (do it recursively).

Bubble-up Operation:

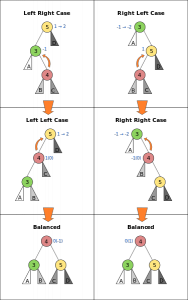
1.If inserted element is smaller than its parent node in case of Min-Heap OR greater than its parent node in case of Max-Heap, swap the element with its parent.
2.Keep repeating the above step, if node reaches its correct position, STOP.

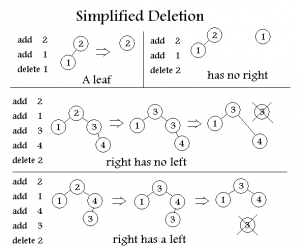
Delete Operation:
1.Find the index for the element to be deleted.
2.Take out the last element from the last level from the heap and replace the index with this element 3.Perform Sink-down.

Sink-Down Operation:
1.If replaced element is greater than any of its child node in case of Min-Heap OR smaller than any if its child node in case of Max-Heap, swap the element with its smallest child(Min-Heap) or with its greatest child(Max-Heap).
2.Keep repeating the above step, if node reaches its correct position, STOP.

Tries
also called digital tree and sometimes radix tree or prefix tree (as they can be searched by prefixes), is an ordered tree data structure that is used to store a dynamic set or associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the key with which it is associated. All the descendants of a node have a common prefix of the string associated with that node, and the root is associated with the empty string. Values are not necessarily associated with every node. Rather, values tend only to be associated with leaves, and with some inner nodes that correspond to keys of interest. For the space-optimized presentation of prefix tree, see compact prefix tree.

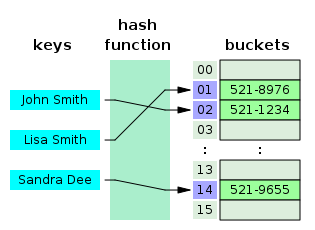
Hashing
a hash table (hash map) is a data structure used to implement an associative array, a structure that can map keys to values. A hash table uses a hash function to compute an index into an array of buckets or slots, from which the desired value can be found.

 

today lesson is gonna more talk about Red Black Tree(RBT) and 2-3 tree that will be explained by the lecturer miss rulyna.

red–black tree(RBT) is a kind of self-balancing binary search tree. Each node of the binary tree has an extra bit, and that bit is often interpreted as the color (red or black) of the node. These color bits are used to ensure the tree remains approximately balanced during insertions and deletions.

RBT rules

1.Insertion
If you want to insert a node in a RBT is very similar insertion like BST only a minor changes like :

1. A root of a node have to be black.
2. the leaf of a RBT have to had red color
   *if you don’t follow these rules your tree must have a violation that have to be fixed in order to balance the tree.

2.Delete
to delete the nodes is use the same principal like BST but the difference is you have to follow those violation rules to balance out your RBT.

Clik here to see RBT visualization

2-3 Tree is a tree data structure, where every node with children (internal node) has either two children (2-node) and one data element or three children (3 nodes) and two data elements. According to Knuth, “a B-tree of order 3 is a 2-3 tree.” Nodes on the outside of the tree (leaf nodes) have no children and one or two data elements. 2−3 trees were invented by John Hopcroft in 1970. 2-3 tree is not categorized as a BST tree.

Rules:
1. 2-3 has 3 key in 1 node.
2. Max child of the tree is 3.
3.The calculation is (n-1/2).
4.every leaf have the same level
Insertion

to insert the nodes first you must determine witch key should be put correctly :
1.smallest amount key on the left.
2.the larger amount key put to the right.
3.the middle key is the amount between the smallest and the large ones

after the key is full you can add another node .
Note: to balance the 2-3 tree you need to pull some of the amount of key in the root to balance out the tree or you can push the amount of key to the root to fill the root node and balance it out .

Delete
To delete a tree first you must find the replacement for the deletion of the tree
1.If the leaf node is 2 – node , if the sibling is a 3 – node , then take one key from one parent and one sibling in a push data from node to a parent .
2.If the leaf node is a 3 – node the the key from the first parent.
3.If the sibling of the leaf node is a 3 – node , then do push 1 data from the sibling to parent.
4.If the sibling of the leaf node is 2 – node , then the parent should be changed to a 2- node , and then do a merge between leaf nodes and sibling nodes.

do it until the 2-3 tree is balance

Today topic is divided by 2 topic the first topic is AVL Tree lectured by Pa Sky and the second is lectured by Selvakumar Manickam

Before we know what AVL tree is first we have to know what is balanced binary search tree.

First Topic

Balanced Binary Search Tree

A self-balancing binary search tree or height-balanced binary search tree is a binary search tree (BST) that attempts to keep its height, or the number of levels of nodes beneath the root, as small as possible at all times, automatically.

example:

Why do we have to learn Balanced Binary Tree?

Most operations on a BST take time proportional to the height of the tree, so it is desirable to keep the height small.

Self-balancing binary trees solve this problem by performing transformations on the tree at key times, in order to reduce the height. Although a certain overhead is involved, it is justified in the long run by ensuring fast execution of later operations.

AVL Tree

AVL tree (Georgy Adelson-Velsky and Evgenii Landis’ tree, named after the inventors) is a self-balancing binary search tree. It was the first such data structure to be invented.[2] In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where n is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.

well to put it simple on how to use a avl tree is to compare the nodes that we want to input and put it in the left side or the right side depends of it’s value of input nodes.

Class AVL Tree supports the following functionality:
1.insertion of a new entry in the tree.
2.removal of any entry in the tree.
3.search for any entry in the tree.
4.”sanity check” for the tree (sanity check is a basic test to quickly evaluate whether a claim or the result of a calculation can possibly be true)
5. 4 various tree traversals
– preorder
– inorder
– postorder
– inorder non-recursive.

How to make a unbalanced BST into Balance BST(AVL)

the main point to make a AVL Tree is to minimum the height of the BST and make the BST stabilize own it self .

1.Calculate the height

-Max (HeightLeft , HeightRight)+1

-Leaf that doesn’t have anymore branch = NULL or 0

2.Balance factor

-Balance factor = HeightLeft – HeightRight
Note:
– if the balance factor is equal to  (-1) that means your balance tree is advancing to the right.
-if the balance factor is equal to (+1) that means that your balance factor is advancing to the left.
-if the balance factor is equal to (0) that means that your balance factor is in balance position
*to be categorized on balance factor the calculation has to be at a number of (-1,0,1)

3.Rotation

Rotation is needed if the total of balance factor is not equal to (-1,0,1)

example

from this picture we know that after we insert the number 7 on the BST the tree becomes unbalanced.

To properly rotate a BST Tree in to a Balanced Tree(AVL)  we hav to the these two rotations :
1.Single Rotation

A single rotation is required when the node just added is on the right sub-tree of the right node of the unbalanced node or the left sub-tree of the left node of the unbalanced node.

2.Double Rotation

A double rotation is required when the node just added is on the right sub-tree of the left node of the unbalanced node or the left sub-tree of the right node of the unbalanced node.

4.Delete

to delete a AVL tree is a little similar like deleting a BST Tree but after you delete your nodes make sure you balance the tree again so the tree stays AVL not BST

Thing you have to watch when you delete a node on AVL tree

-Check the height and the balance factor.
-do a rotation if necessary

These examples have been greatly simplified from the actual amount of work required. All of these examples could have more children on almost every node, which would require a greater deal of reassigning pointers.

For more understanding how these concept that i have shown you open here
->AVL Tree Visualzation

Second Topic

As for the second topic the lesson is about the general meaning of data structure , introduction of tree , and discuss about binary tree. These topics is lectured by a guest lecture named Selvakumar Manickam .

for these materials it generally talks about the point of studying data structure as the basic for studying Tree and the principal of studying all kind of tree in programming for more detailed information you can see my older post below:

Summary Session 1 Data Structures
(The general meaning of Data Structures in computer Programming)
Summary Session 4 Data Structures
(Tree indroduction)
Summary Session 5 Data Structures
(More information about tree)