Today lesson is gonna more to talk about binary tree that will bi explain by the lecturer pak sky
Binary Tree
A binary tree is made of nodes, where each node contains a “left” pointer, a “right” pointer, and a data element. The “root” pointer points to the topmost node in the tree. The left and right pointers recursively point to smaller “subtrees” on either side. A null pointer represents a binary tree with no elements — the empty tree
Binary Search Tree
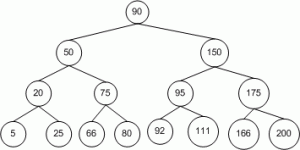
A binary search tree is a rooted binary tree, whose internal nodes each store a key (and optionally, an associated value) and each have two distinguished sub-trees, commonly denoted left and right. The tree additionally satisfies the binary search tree property, which states that the key in each node must be greater than all keys stored in the left sub-tree, and smaller than all keys in right sub-tree.
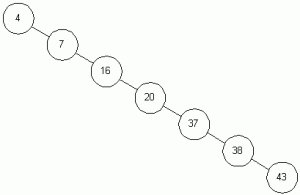
Unbalanced Tree
an unbalance tree is a binary search three that doesn’t follow the theory of a balance tree that can couse the binary tree un balanced .
To solve this problem there are two wasy to fix an unbalanced tree there are:
1.AVL Tree
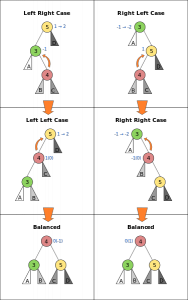
AVL tree (Georgy Adelson-Velsky and Evgenii Landis’ tree, named after the inventors) is a self-balancing binary search tree. It was the first such data structure to be invented.[2] In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where n is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.
well to put it simple on how to use a avl tree is to compare the nodes that we want to input and put it in the left side or the right side depends of it’s value of input nodes.
2.Red Black Tree
A red–black tree is a kind of self-balancing binary search tree. Each node of the binary tree has an extra bit, and that bit is often interpreted as the color (red or black) of the node. These color bits are used to ensure the tree remains approximately balanced during insertions and deletions.
Balance is preserved by painting each node of the tree with one of two colors (typically called ‘red’ and ‘black’) in a way that satisfies certain properties, which collectively constrain how unbalanced the tree can become in the worst case. When the tree is modified, the new tree is subsequently rearranged and repainted to restore the coloring properties. The properties are designed in such a way that this rearranging and recoloring can be performed efficiently.